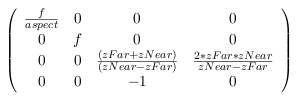|
Aktuelle Zeit: Sa Feb 14, 2026 21:30 Foren-Übersicht » Programmierung » Einsteiger-Fragen |
Unbeantwortete Themen | Aktive Themen |
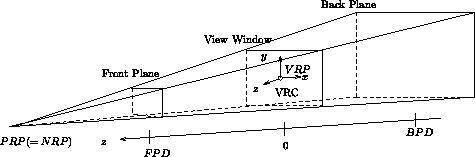
Einige Fragen zur Viewing Pipeline
Moderator: DGL-Team
|
|
Seite 1 von 1 |
[ 13 Beiträge ] |
|
| Autor | Nachricht | ||||
|---|---|---|---|---|---|
| m.sirin |
|
||||
Registriert: Fr Jul 16, 2010 18:28 Beiträge: 40 |
|
||||
| Nach oben | |||||
| sharkman |
|
|||||
Registriert: Fr Dez 11, 2009 08:02 Beiträge: 532 Programmiersprache: pascal (Delphi 7) |
|
|||||
| Nach oben | ||||||
| Coolcat |
|
|||||
Registriert: Do Dez 29, 2005 12:28 Beiträge: 2249 Wohnort: Düsseldorf Programmiersprache: C++, C#, Java |
|
|||||
| Nach oben | ||||||
| sharkman |
|
|||||
Registriert: Fr Dez 11, 2009 08:02 Beiträge: 532 Programmiersprache: pascal (Delphi 7) |
|
|||||
| Nach oben | ||||||
| Coolcat |
|
|||||
Registriert: Do Dez 29, 2005 12:28 Beiträge: 2249 Wohnort: Düsseldorf Programmiersprache: C++, C#, Java |
|
|||||
| Nach oben | ||||||
| m.sirin |
|
||||
Registriert: Fr Jul 16, 2010 18:28 Beiträge: 40 |
|
||||
| Nach oben | |||||
| Coolcat |
|
|||||
Registriert: Do Dez 29, 2005 12:28 Beiträge: 2249 Wohnort: Düsseldorf Programmiersprache: C++, C#, Java |
|
|||||
| Nach oben | ||||||
| sharkman |
|
|||||
Registriert: Fr Dez 11, 2009 08:02 Beiträge: 532 Programmiersprache: pascal (Delphi 7) |
|
|||||
| Nach oben | ||||||
| Traude |
|
|||||
Registriert: Di Okt 03, 2006 14:07 Beiträge: 1277 Wohnort: Wien |
|
|||||
| Nach oben | ||||||
| Coolcat |
|
|||||
Registriert: Do Dez 29, 2005 12:28 Beiträge: 2249 Wohnort: Düsseldorf Programmiersprache: C++, C#, Java |
|
|||||
| Nach oben | ||||||
| sharkman |
|
|||||
Registriert: Fr Dez 11, 2009 08:02 Beiträge: 532 Programmiersprache: pascal (Delphi 7) |
|
|||||
| Nach oben | ||||||
| m.sirin |
|
||||
Registriert: Fr Jul 16, 2010 18:28 Beiträge: 40 |
|
||||
| Nach oben | |||||
| Coolcat |
|
|||||
Registriert: Do Dez 29, 2005 12:28 Beiträge: 2249 Wohnort: Düsseldorf Programmiersprache: C++, C#, Java |
|
|||||
| Nach oben | ||||||
|
|
Seite 1 von 1 |
[ 13 Beiträge ] |
Wer ist online? |
Mitglieder in diesem Forum: Baidu [Spider] und 10 Gäste |
| Du darfst keine neuen Themen in diesem Forum erstellen. Du darfst keine Antworten zu Themen in diesem Forum erstellen. Du darfst deine Beiträge in diesem Forum nicht ändern. Du darfst deine Beiträge in diesem Forum nicht löschen. Du darfst keine Dateianhänge in diesem Forum erstellen. |